Enhancements to Analysis Capabilities

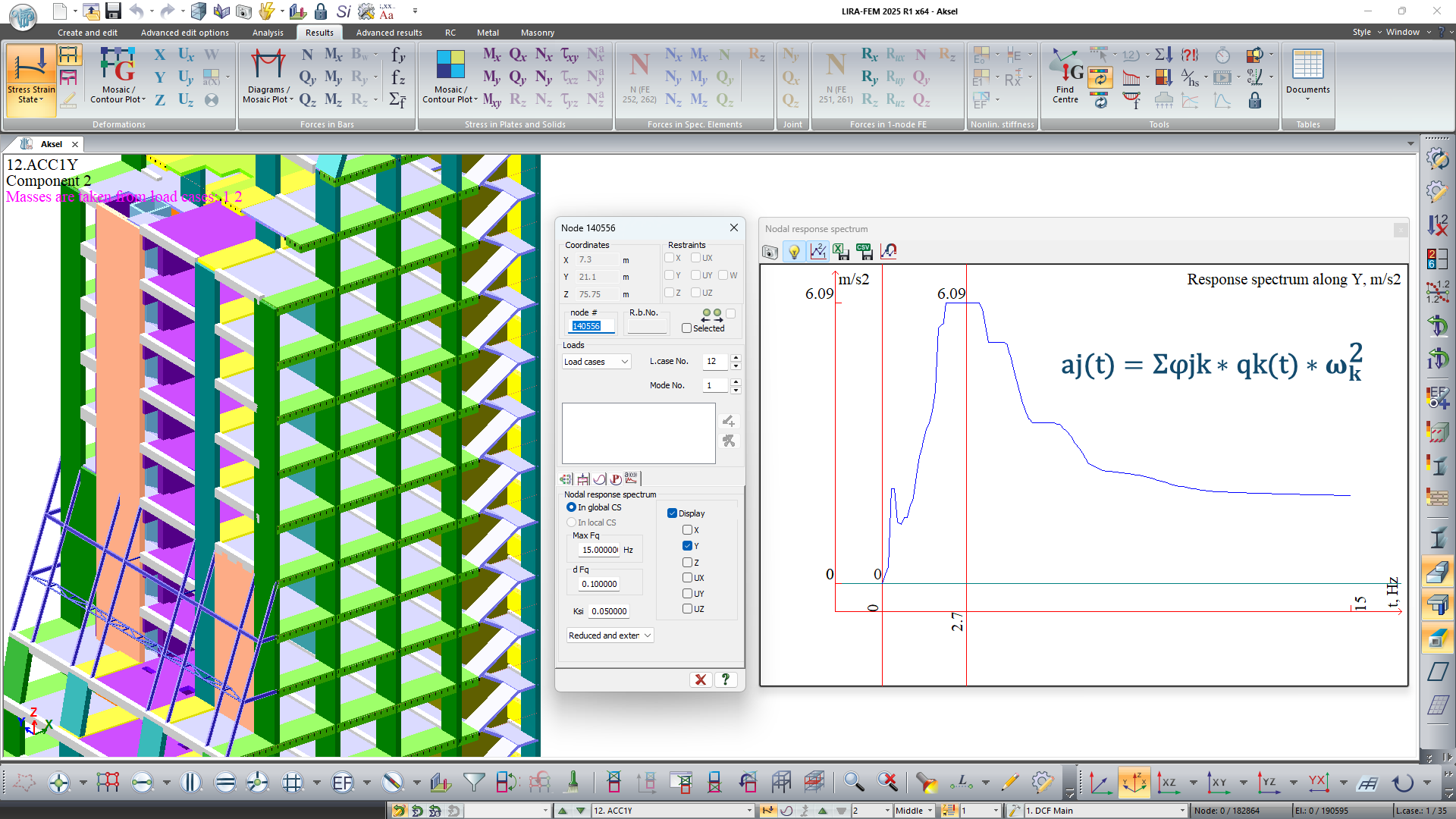
When generating response spectrum graphs using module 27, the approach for determining the final accelerations—taking into account all mode shapes on which the spectrum is based—has been adjusted.

Now the spectrum is generated based on the graph of pseudo-acceleration changes (floor accelerogram), where the acceleration at each moment is determined as follows:

aj(t) = ΣΔjk * qk(t) * ωk²,

where aj(t) is the acceleration of the j-th degree of freedom at time t,
Δjk is the ordinate of the j-th degree of freedom for the k-th mode,
qk(t) is the generalized coordinate for the k-th vibration mode at time t,
ωk is the circular frequency for the k-th vibration mode.

This approach produces results analogous to those obtained by direct integration of the equations of motion in geometric coordinates.

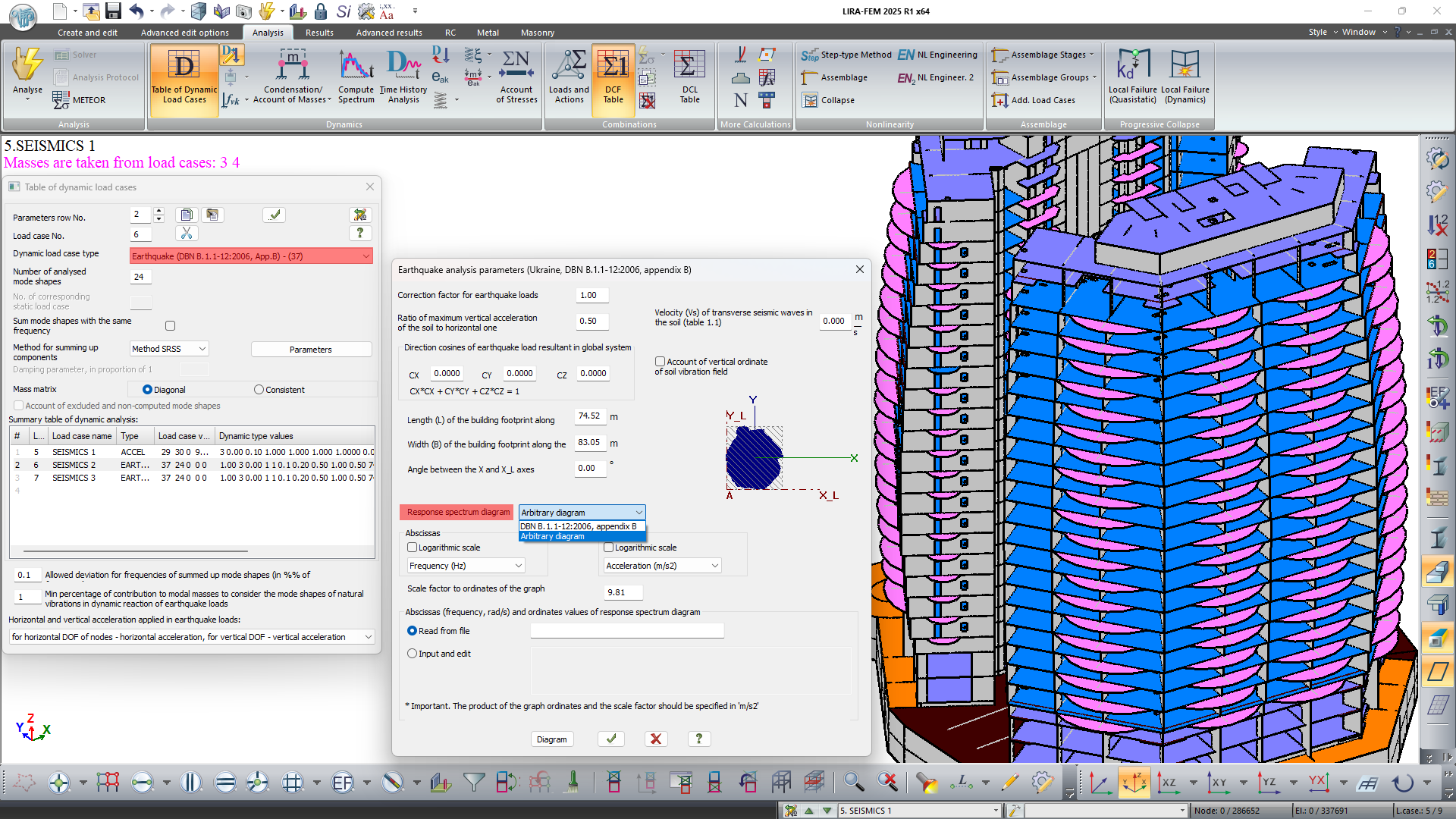
In the new version of dynamic module 37 (DBN V.1.1-12:2006, Appendix V), the option to use an arbitrary response spectrum graph in analyses has been introduced.

Dynamic module 37 allows one to account for the non-uniformity of the ground vibration field in analysis on earthquake loads. This model of earthquake analysis makes it possible to account for the spatial characteristics of structures with irregular layouts according to the propagation scheme of the seismic wave.

This model assumes that the plan of the structure is inscribed in a rectangular area of length L and width B. The propagating seismic wave moves along the long side, causing translational, rotational, and bending vibrations of the structure.

The effect of the seismic wave on the inertial seismic force magnitudes is taken into account using the ordinates of the ground vibration field fk1, fk2, fk3, which are introduced into the formula for the distribution coefficient ηki.

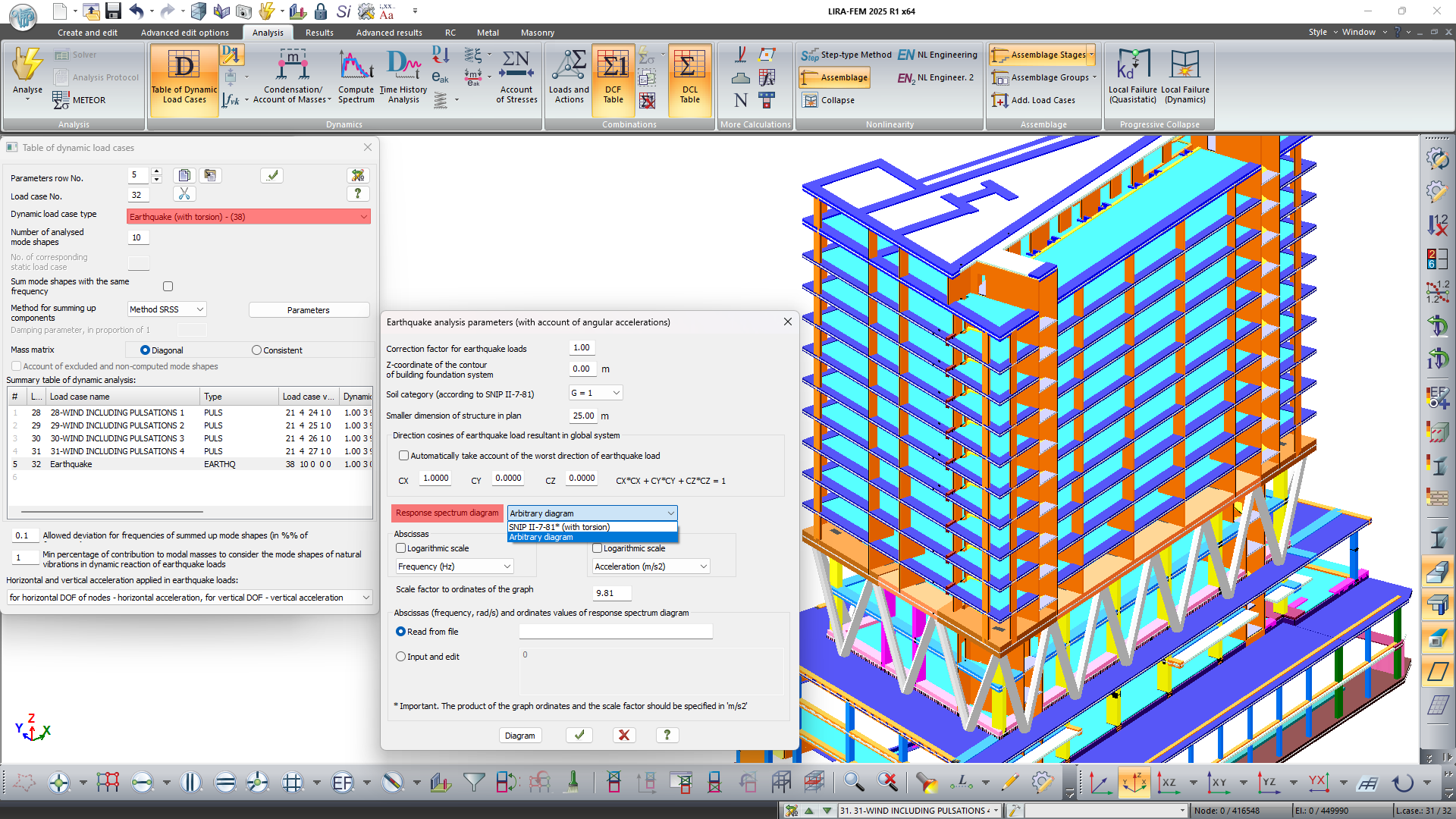
In module 38 (SNIP II-7-81 as amended on 01.01.2000 with torsion considerations), the option to use an arbitrary response spectrum graph in calculations has been added. The integrated model for analysis on earthquake load accounts for the movement of the ground mass under the structure as a single unit. This movement is determined by the vector of translational acceleration and the vector of angular acceleration of rotation.

It is assumed that these vectors are random both in time and space and are defined by the respective parameters. If the cosines for the translational impact vector are specified, then the direction of the angular acceleration vector is automatically calculated as orthogonal to the translational vector. The distribution coefficient in the calculation allows for obtaining inertial seismic forces not only for translational but also for torsional mode shapes.

The algorithm for the automatic selection of the step for geometrically nonlinear problems has been modernized.

An option has been added for the response spectrum graphs to set the output format of the abscissa values as oscillation frequency or period.

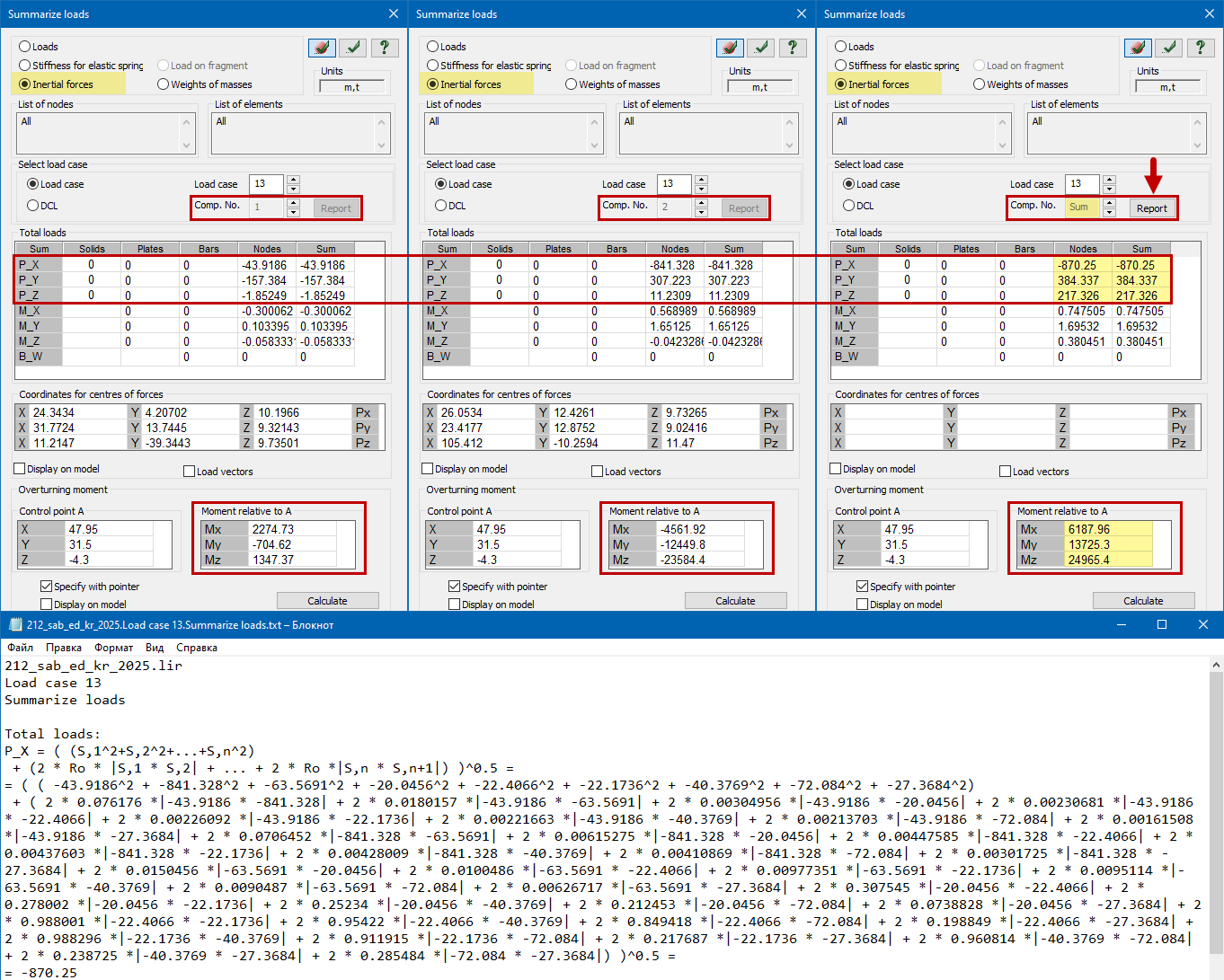
In the analysis results, on the "Summarize loads" menu, functionality has been added to determine the total shear forces and overturning moment from dynamic loads (earthquake and pulsation) for shear and overturning calculations. The summation is performed using the same method (SSRS, CQC, 10%) selected in the dynamic action parameters. A detailed report can be generated based on the summation results for verification and/or documentation purposes.